ACS6116-Rocket-Landing-MPC

ACS6116—Rocket-Landing-MPC-

An assignment set for the ACS6116 - Advanced Control module. The assignment focussed on modelling and controlling a Falcon 9 rocket during landing, using constrained and unconstrained model predictive control (MPC) techniques. Model Predictive Control (MPC) is an advanced control technique where inputs are recalculated every time step, based on an optimal control procedure. This work aimed to bridge the gap between theoretical control concepts and their application in managing the complex dynamics of a rocket’s descent. The essence of the project was to ensure precision and stability in the landing phase, a challenge that addressed the rocket landing problem using advanced control techniques.

The Objective

Model a point mass rocket, and land it at the coordinates $\vec r(k_f)=(0, 0, 0)$.

The Model

\(\begin{bmatrix} r_x(k+1)\\ r_y(k+1)\\ r_z(k+1)\\ v_x(k+1)\\ v_y(k+1)\\ v_z(k+1)\\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & T_s & 0 & 0\\ 0 & 1 & 0 & 0 & T_s & 0\\ 0 & 0 & 1 & 0 & 0 & T_s\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_x(k)\\ r_y(k)\\ r_z(k)\\ v_x(k)\\ v_y(k)\\ v_z(k)\\ \end{bmatrix} + \begin{bmatrix} \frac{T_s^2}{2m} & 0 & 0\\ 0 & \frac{T_s^2}{2m} & 0\\ 0 & 0 & \frac{T_s^2}{2m}\\ T_s & 0 & 0\\ 0 & T_s & 0\\ 0 & 0 & T_s \end{bmatrix} \begin{bmatrix} f_x(k)+w_x\\ f_y(k)+w_y\\ f_z(k)-mg\\ \end{bmatrix}\)

MPC Setup & Unconstrained Optimisation

I started with the conception of an unconstrained MPC controller. Here, I focused on selecting the appropriate Q and R matrices, emphasizing the significance of vertical position and velocity to avoid hard landings, while treating control efforts, such as fuel consumption, with less priority. This initial phase laid the groundwork, allowing me to establish a baseline control strategy.

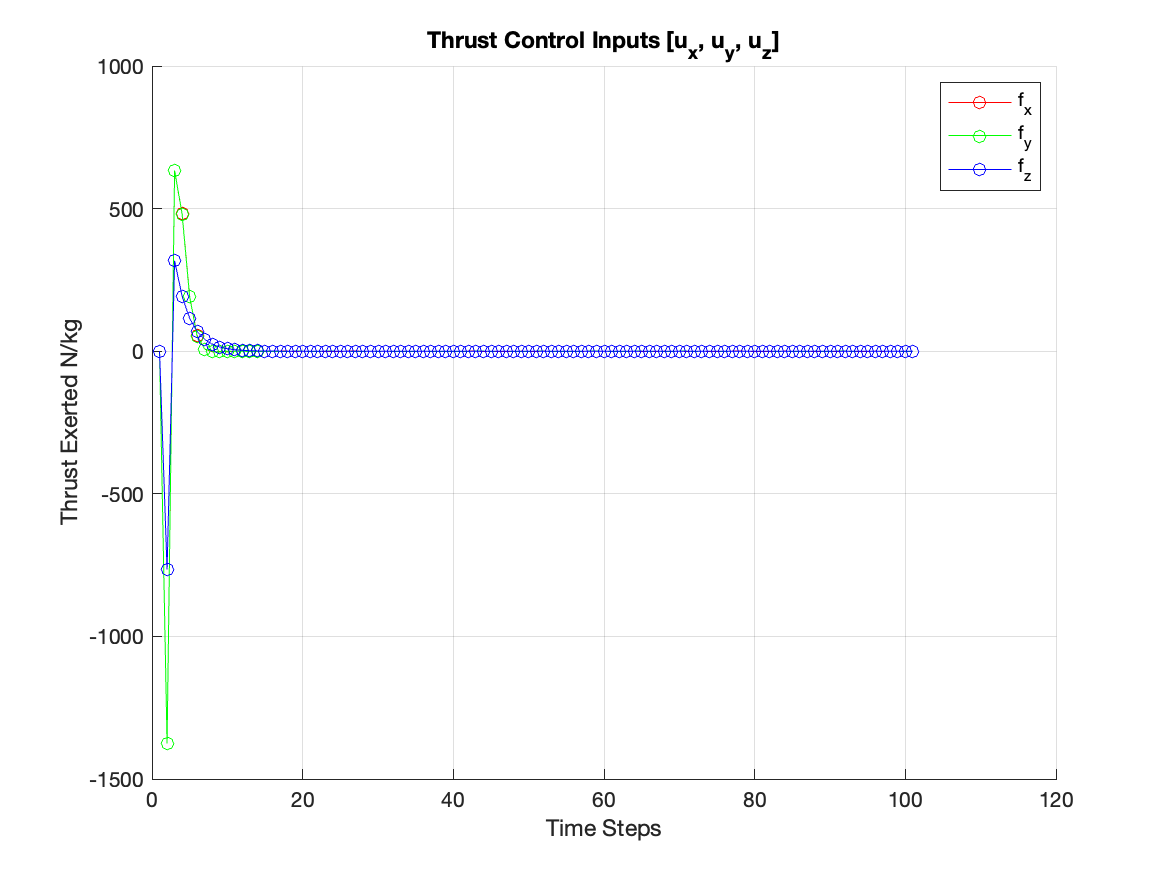
Constrained Optimisation

The introduction of constraints quickly became crucial. The second iteration of the controller incorporated constraints for engine thrust and angle, marking a leap towards a more realistic scenario. These limits ensured the rocket’s manoeuvres remained within feasible operational bounds, such as acceptable engine thrust angles and glide slope angles.

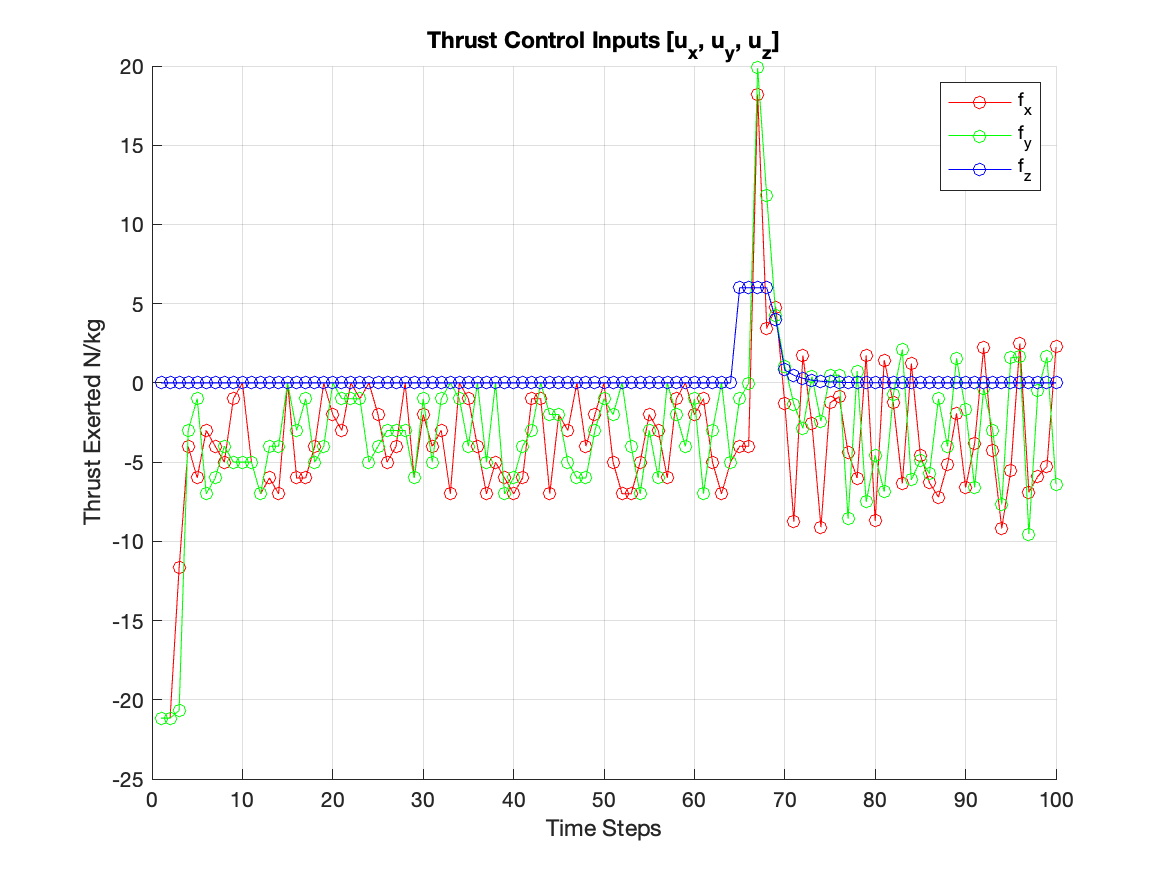
Disturbance Rejection

To further increase realism in the rocket landing scenario, integrating disturbance rejection capabilities to counteract environmental influences, particularly wind disturbances, became a priority. This final enhancement was not just about adding another layer of complexity; it was about building resilience into the system, which now could maintain its trajectory under unpredictable conditions.

https://github.com/sebzuddas/ACS6116-Rocket-Landing-MPC/assets/62427628/094f4dfe-9e9c-47ec-97c9-746675503f28